7 Sided Polygon Exterior Angles
Angles In A Polygon
Math Facts A Heptagon Is A 7 Sided Polygon With Interior Angles That Add To 900 Degrees Math Facts Heptagon Interior
Angles In A Polygon
What Is The Measure Of A 7 Sided Regular Polygon Quora
Math Facts A Nonagon Is A 9 Sided Polygon With Interior Angles That Add To 1260 Degrees Decorating Apps Math Facts Decoration Website
Math Facts An Octagon Is An 8 Sided Polygon With Interior Angles That Add To 1080 Degrees Math Facts Facts Polygon
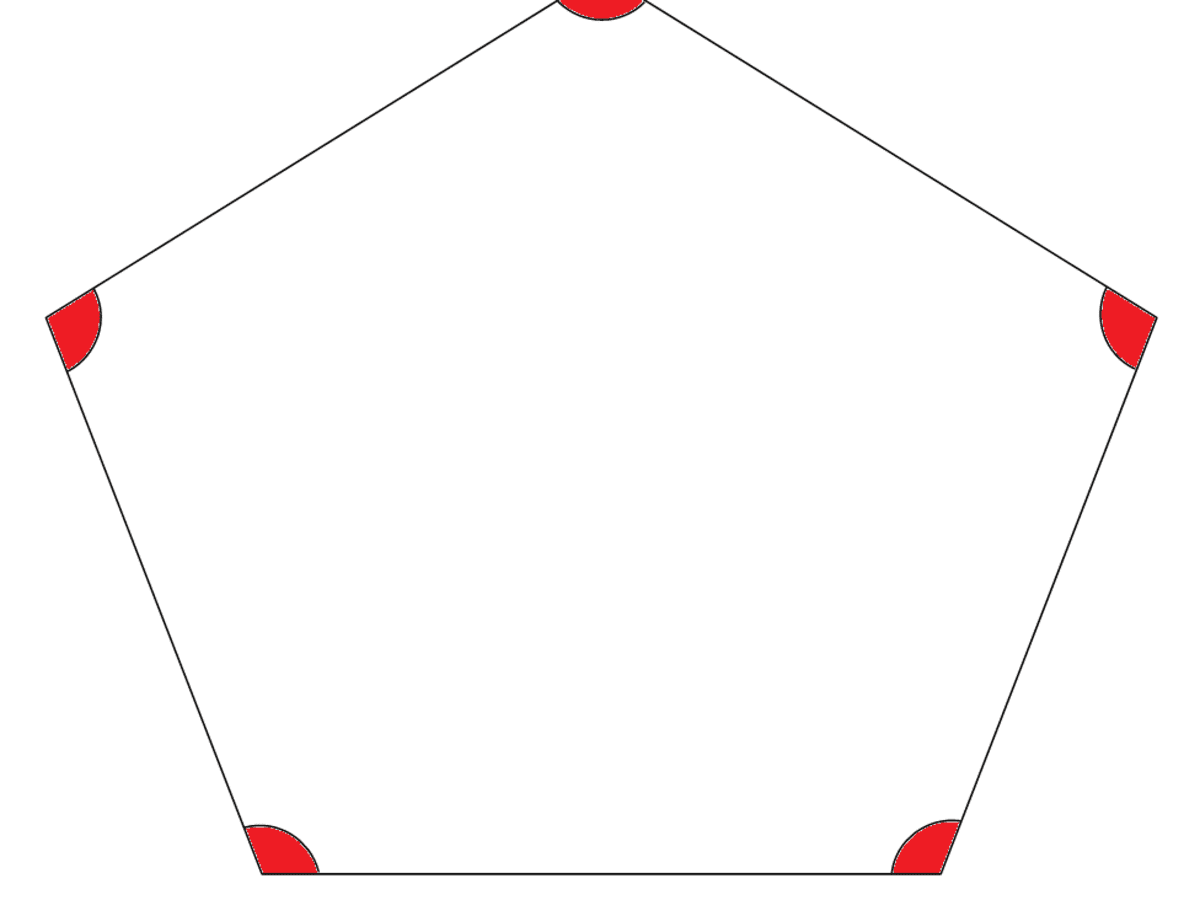
Exterior Angles of Polygons The Exterior Angle is the angle between any side of a shape and a line extended from the next side.
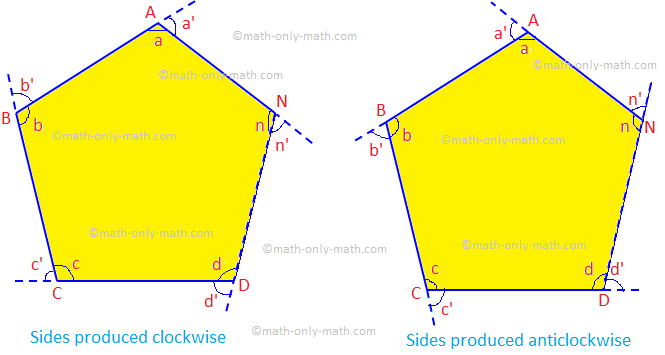
7 sided polygon exterior angles. The exterior angles of this pentagon are formed by extending its adjacent sides. In the case of a regular heptagon each exterior angle 3607 5142857143 deg. As a demonstration of this drag any vertex towards the center of the polygon.
Since you are extending a side of the polygon that exterior angle must necessarily be supplementary to the polygons interior angle. So you can divide 360 by 7 514 degrees to get the exterior angle. You will see that the angles combine to a full 360 circle.
Sum of angles 7 - 2 180. Now for a regular polygon each exterior angle should have the same value. 360 5 72 x 72 2 of 5 Cant edit this PDF.
Therefore The number of heptagon sides 7. Therefore these angles are formed as in the following diagram. The sum of exterior angles is 360.
For example for a pentagon we have. Measure of each exterior angle of 7 sided polygon 3607. All the sides of a heptagon meet with each other end to end to form a shape.
Here exterior angles x 60 Number of sides 36060 6 Therefore there are 6 sides of the regular polygon. As you can see for regular polygons all the exterior angles are the same and like all polygons they add to 360 see note below. They are Supplementary Angles.
Dodecagon Dodecagon Regular Polygon Polygon
A Heptagonal Triangle With Angles P 7 2p 7 And 4p 7 Unfolds To An Irregular 14 Sided Polygon Topology Math Geometry
Chapter 6 Polygons Definitions Polygon Many Sided Figure 3 Sided Triangles 4 Sided Quadrilaterals 5 Sided Pentagons 6 Quadrilaterals Pentagon Hexagon
Maths How To Find Exterior Angle Sum Of A Polygon English Youtube
What Do The Angles In A Polygon Add Up To Owlcation
Sum Of The Exterior Angles Of An N Sided Polygon Solved Examples
Polygons Polygon Quadrilaterals Geometry Formulas
Geometry Worksheets Quadrilaterals And Polygons Worksheets Geometry Worksheets Naming Polygons Regular Polygon
Math Facts A Decagon Is A 10 Sided Polygon With Interior Angles That Add To 1440 Degrees Math Facts Decagon Polygon
Exterior Angles In Convex Polygons Read Geometry Ck 12 Foundation
Polygons Maths Poster Math Poster Teaching Math Studying Math
The Internal Angle And The Sum Of The Internal Angles In Any N Sided Polygon Mathematics Stack Exchange
Unit 15 Section 2 Angle Properties Of Polygons
