Exterior Angle Sum Conjecture

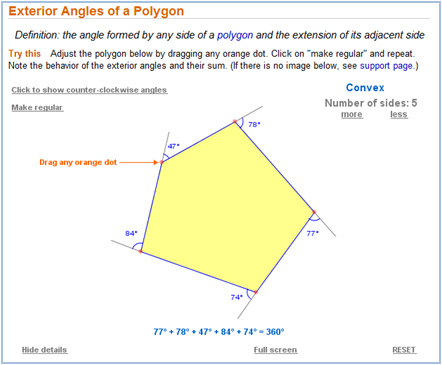
The sum of the n exterior angles for any convex polygon with n sides is 360 degrees.

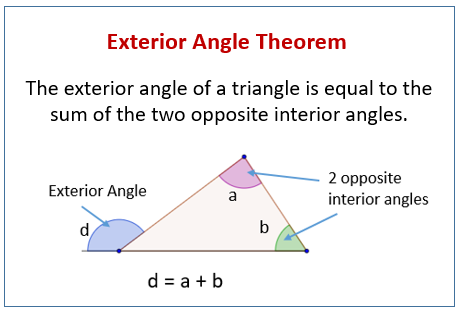
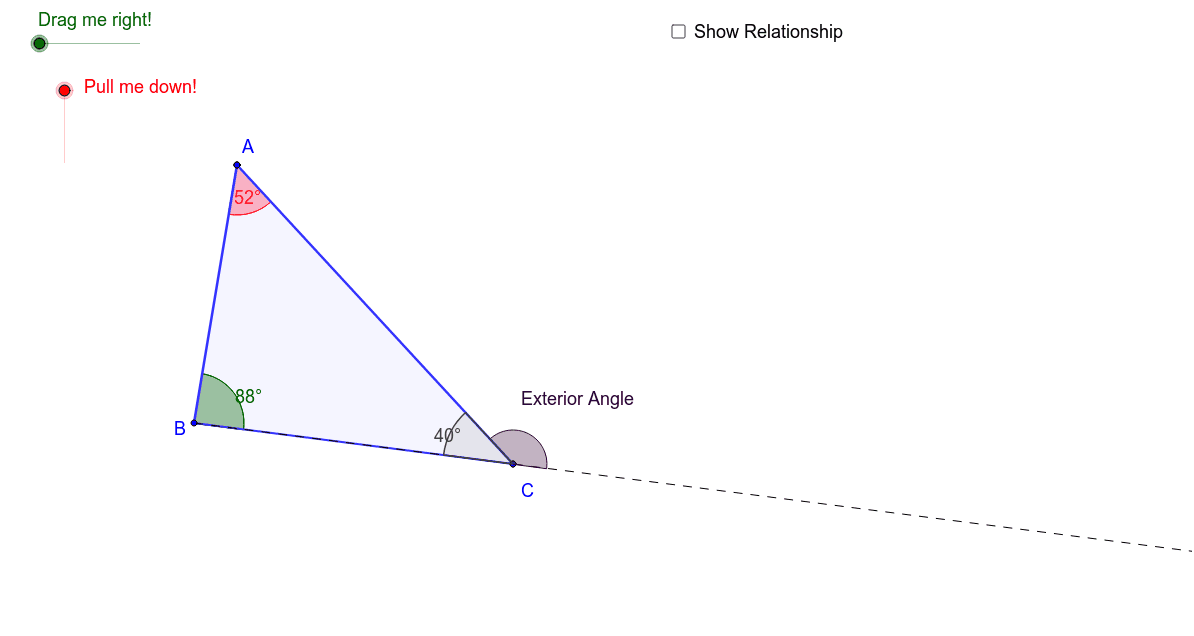
Exterior angle sum conjecture. The sum of an interior angle and the exterior angle of one side of a polygon is equal to 180 since both the angles lie in a straight line. The exterior angle theorem tells us that any exterior angle of a triangle equals the sum of the opposite two interior angles and that the sum of all three interior angles of a triangle equals 180 the sum of two right angles triangle sum theorem. To find the value of a given exterior angle of a regular polygon simply divide 360 by the number of sides or angles that the polygon has.

Therefore N 180n 180n-2 N 180n 180n 360. Corollary Exterior Angle Measures for Regular n-gons. Here is a list of a few important points on the angle sum theorem.

Angle sum theorem holds for all types of triangles. Corollary Exterior Angle Measures for Regular n-gonsEach exterior angle for a regular n-gon has measure equal to 360n degrees. Corollary Exterior Angle Measures for Regular n-gons.

8Worksheet triangle sum and exterior angle theorem answer key author. The sum of the exterior angles of a regular polygon will always equal 360 degrees. Every triangle will have the following properties.

The triangle sum and exterior angle theorem worksheet is a very easy to use worksheet that includes easy to understand explanation for each multiplication. The sum of the n exterior angles for any convex polygon with n sides is 360 degrees. Polygon Exterior Angle Sum Theorem If a polygon is convex then the sum of the measures of the exterior angles one at each vertex is 360.

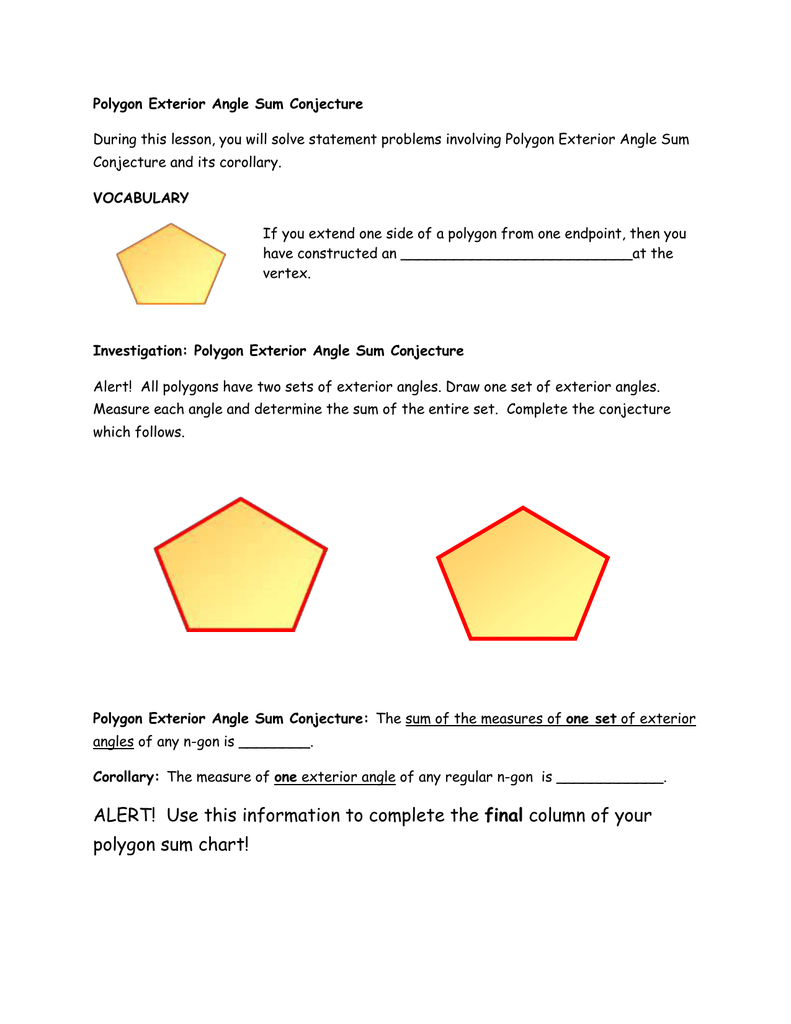
No matter how fussy and multi-sided the regular polygon gets the sum of its exterior angles is always 360. The sum of the two opposite interior angles equals the exteri. After each member of the group traces all of the exterior angles so that they are adjacent the group compares their results to conjecture about the exterior angle sum for any polygon.