Find The Sum Of Exterior Angles Of A Polygon
Polygon Interior Angle Sum Exterior Angle Sum Theorems Doodle Notes Interior And Exterior Angles Exterior Angles Graphic Organizers
Polygons Graphic Organizer And Practice Middle School Math Geometry Graphic Organizers Geometry Worksheets
Pin By Larissa Jones On Math Teaching Geometry Math Interactive Notebook Math Geometry
11 Angle Sum Of Any Polygon Maths Tutorials Youtube Math Tutorials Math For Kids Math
Interior And Exterior Angles Of Polygons Teaching Resources Interior And Exterior Angles Exterior Angles Angles Worksheet
Polygon Angle Riddle Time Exterior Angles Interior And Exterior Angles Riddles
Thus 70 60 65 40 x 360 235 x 360 X 360 235 125 Example 2.
Find the sum of exterior angles of a polygon. The sides of the polygon meet at the vertices forming angles. Also the measure of each exterior angle of an equiangular polygon 360n. Therefore all its exterior angles measure the same as well that is 120.
One important property about a regular polygons exterior angles is that the sum of the measures of the exterior angles of a. The sum of the exterior angles of a regular polygon will always equal 360 degrees. 1Find the exterior angle of a regular octagon.
They are Supplementary Angles. Extend each side of the polygon forming an exterior angle at each vertex. A Polygon is any flat shape with straight sides.
In geometry an icosidigon or icosikaidigon or 22-gon is a twenty-two-sided polygon. To find the value of a given exterior angle of a regular polygon simply divide 360 by the number of sides or angles that the polygon has. Thus the sum of exterior angles can be obtained from the following formula.
7 rows Since the sum of exterior angles of any polygon is always equal to 360 we can divide by. For any closed structure formed by sides and vertex the sum of the exterior angles is always equal to the sum of linear pairs and sum of interior angles. 2What is the polygon whose sum of interior angles is 1800.
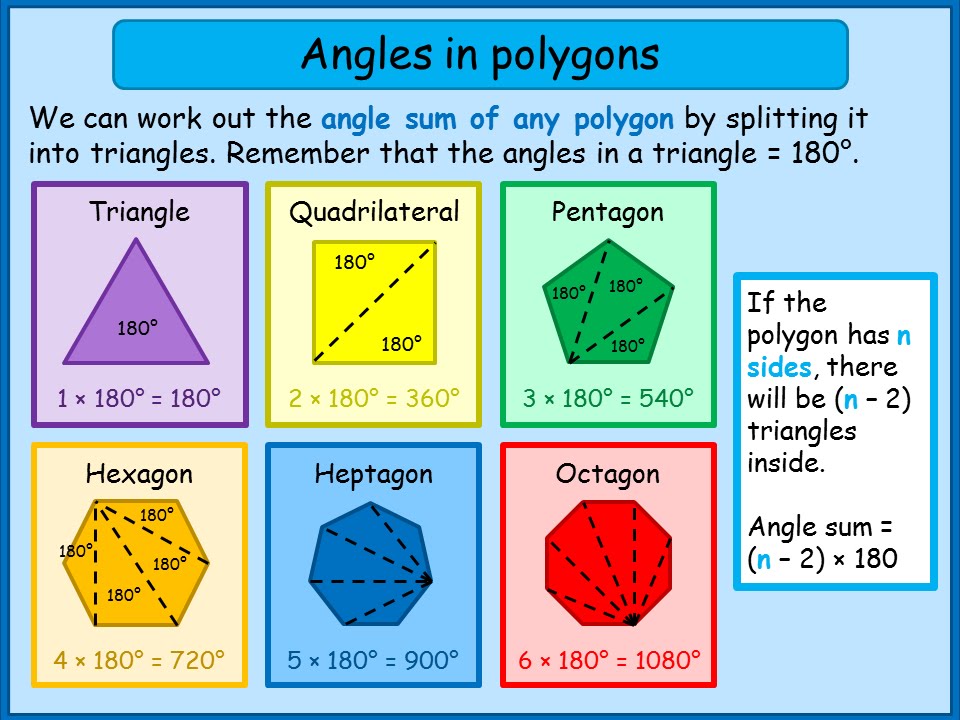
The sum of the measures of the interior angle of any polygon is the number of sides minus 2 multiplied by 180. Therefore we can calculate the measure of one of the exterior angles of a regular polygon by dividing 360 by the number of sides of the regular polygon. Find the sum of exterior angles obtained on producing in order the sides of a polygon with.
Chic Missing Angles Worksheet Ks3 Tes For Interior Angles Of A Polygon Worksheet Tes Angles Worksheet Polygon Regular Polygon
Interior Angles Of Polygons Mr Mathematics Com Polygon Exterior Angles Angles
Exterior Angles Of A Polygon Geometry Activity Finding The Sum Teaching Geometry Geometry Activities Math Geometry
Polygons Reference Sheet Interior Exterior Angle Sum Area Math Notes School Organization Notes School Notes
Gcse Revision Checklists Gcse Math Studying Math Gcse In 2021 Regular Polygon Studying Math Angles Math
Interior Exterior Angles Of Polygons Maze Beginner Interior And Exterior Angles Exterior Angles Middle School Math Geometry
Polygon Clipart Geometry Angle Pencil And In Color In 2021 Geometry Angles Hexagon Angles Interior And Exterior Angles
Interior Exterior Angles Of Polygons Worksheet Maze Activity Interior And Exterior Angles Exterior Angles Geometry Worksheets
Polygon Angle Exploration Interior And Exterior Angles Regular Polygon Polygon
Pin On Science Yay And Stem Science Technology Engineering Math
Polygon And Angles Worksheet Fresh Basic Geometry Chessmuseum Template Library In 2021 Angles Worksheet Regular Polygon Word Problem Worksheets
Interior And Exterior Angles Of Polygons Ws Interior And Exterior Angles Exterior Angles Middle School Math Geometry
11 Angle Sum Of Any Polygon Maths Tutorials Youtube Math Tutorials Math For Kids Math
