Formula For The Sum Of Exterior Angles Of A Polygon
Polygon Interior Angle Sum Exterior Angle Sum Theorems Doodle Notes Interior And Exterior Angles Exterior Angles Graphic Organizers
11 Angle Sum Of Any Polygon Maths Tutorials Youtube Math Tutorials Math For Kids Math
Gcse Revision Checklists Gcse Math Studying Math Gcse In 2021 Regular Polygon Studying Math Angles Math
Polygon Clipart Geometry Angle Pencil And In Color In 2021 Geometry Angles Hexagon Angles Interior And Exterior Angles
11 Angle Sum Of Any Polygon Maths Tutorials Youtube Math Tutorials Math For Kids Math
Interior Angles Of Polygons Mr Mathematics Com Polygon Exterior Angles Angles
Exterior angle of a polygon 360 number of sides.
Formula for the sum of exterior angles of a polygon. The sum of exterior angles of a polygon is 360. The formula for calculating the size of an exterior angle in a regular polygon is. 360 div number of sides.
360 6 60 the size of an exterior angle 180 60 120 x 120 Example 2. We know that the sum of exterior angles of a polygon is 360 degrees. TextExterior angle dfrac360circn where eqn eq is the number of.
Sum of angles of a square. So the measure of each exterior angle will be 18 0 o n 2 18 0 o n. C The sum of the interior angles in any polygon can be found by multiplying the number of triangles formed by the diagonals from one.
Now the sum of exterior angles 36 0 o n n 36 0 o. 18 0 o n n 2 18 0 o n. Round your answer to the nearest tenth if necessary.
Identify the type of regular polygon whose exterior angle measures 120 degrees. Therefore the sum of exterior angles 360 Proof. Therefore all its exterior angles measure the same as well that is 120.
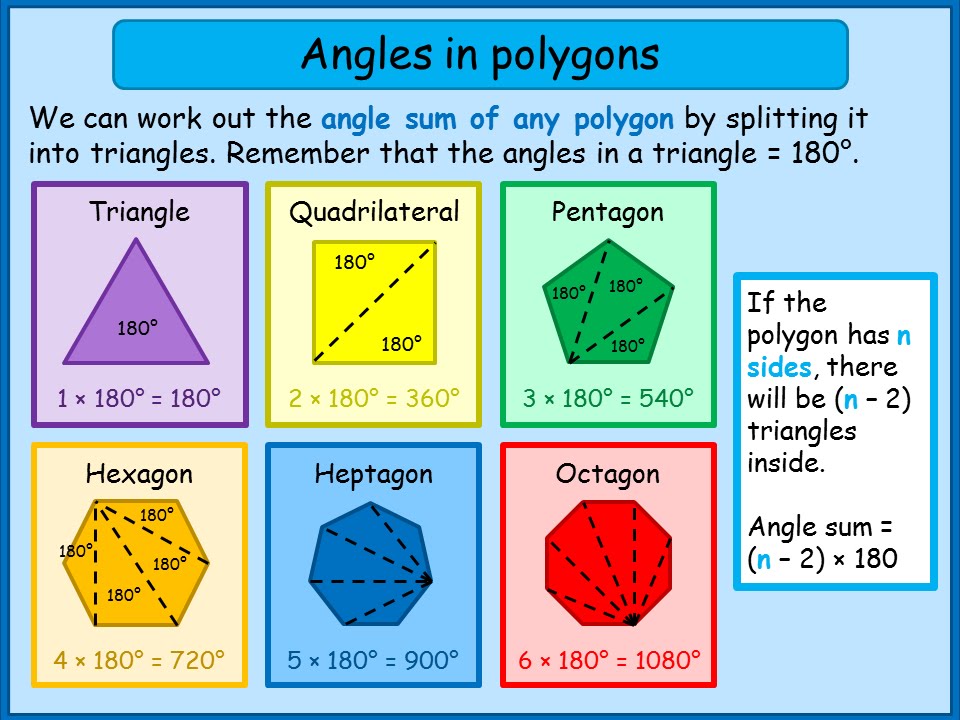
To find the sum of the interior angles multiply the number of triangles by 180. N-2 5401803 n5 so each exterior angle 360572. Since the polygon is regular we can use the sum obtained in the previous example and divide by 11 since all the angles are equal.
Polygons Reference Sheet Interior Exterior Angle Sum Area Math Notes School Organization Notes School Notes
Pin On Homedecor
Pin By Waji On Interior Paint Simulator Theorems Exterior Angles Angles
Pin By Waji On Interior Paint Simulator Exterior Angles Theorems Interior Design Programs
Pin By Towice On Exterior Angle Theorem Exterior Angles Interior And Exterior Angles Angles
Pin On Science Yay And Stem Science Technology Engineering Math
Pin Oleh Towice Di Exterior Angle Theorem
Chic Missing Angles Worksheet Ks3 Tes For Interior Angles Of A Polygon Worksheet Tes Angles Worksheet Polygon Regular Polygon
Pin On Homedecor
Pin By Towice On Exterior Angle Theorem Exterior Angles Interior And Exterior Angles Angles
Polygons Maths Poster Math Poster Teaching Math Studying Math
Polygons Reference Sheet Interior Exterior Angle Sum Area Math Notes School Organization Notes School Notes
Angles And Polygons Interior And Exterior Angles Exterior Angles Interior Design School
