Sum Of Exterior Angles Of A Square
Learning Card For Exterior Angle Sum Property Of A Quadrilateral Quadrilaterals Mathematics Learning Cards
Polygon Clipart Geometry Angle Pencil And In Color In 2021 Geometry Angles Hexagon Angles Interior And Exterior Angles
Interior And Exterior Angles Of Polygons Teaching Resources Interior And Exterior Angles Exterior Angles Angles Worksheet
Polygons Graphic Organizer And Practice Middle School Math Geometry Graphic Organizers Geometry Worksheets
Chic Missing Angles Worksheet Ks3 Tes For Interior Angles Of A Polygon Worksheet Tes Angles Worksheet Polygon Regular Polygon
Pin By Larissa Jones On Math Teaching Geometry Math Interactive Notebook Math Geometry
First determine the number of sides.
Sum of exterior angles of a square. To find the measure of a single exterior angle we simply divide the measure of sum of the exterior angles with the total number of sides. For example a square would have 4 sides and a pentagon would have 5 sides. What is the formula for finding exterior angles of a polygon.
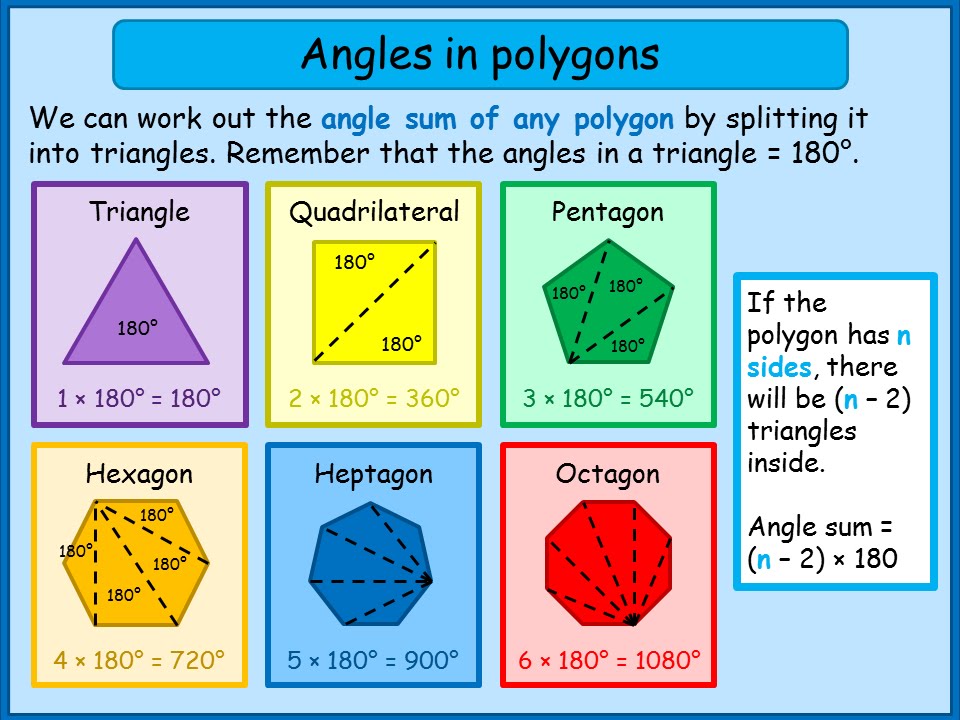
Sum of exterior angles n x 180 n-2 x 180 n x 180 n x 180 2 x 180 180n 180n 360 360 Hence Sum of the exterior angles of any polygon is 360. For any closed structure formed by sides and vertex the sum of the exterior angles is always equal to the sum of linear pairs and sum of interior angles. The sum of exterior angles of a given polygon 360.
A Polygon is any flat shape with straight sides. To find the value of a given exterior angle of a regular polygon simply divide 360 by the number of sides or angles that the polygon has. Interior angles are 90 deg.
N - 2 180. Exterior Angles Examples Multiply each of those measurements times the number of sides of the regular polygon. The two exterior angles that can be formed at a vertex by extending alternately one side or the other are vertical angles and thus are equal.
The sum of the exterior angle of all polygon. Let us check a few solved examples to learn more about the sum of exterior angles formula. For example for a pentagon this would equal 5-2180 3.
Interior angles are 120. When we add up the Interior Angle and Exterior Angle we get a straight line 180. In the same way we can prove that the sum of all exterior angles of any polygon is 360.
11 Angle Sum Of Any Polygon Maths Tutorials Youtube Math Tutorials Math For Kids Math
Interior Angles Of Polygons Mr Mathematics Com Polygon Exterior Angles Angles
11 Angle Sum Of Any Polygon Maths Tutorials Youtube Math Tutorials Math For Kids Math
Polygon Interior Angle Sum Exterior Angle Sum Theorems Doodle Notes Interior And Exterior Angles Exterior Angles Graphic Organizers
Angles Triangles Geometry Tutorial Math Tutorials Triangle Math Geometry Notes
Pin By Waji On Interior Paint Simulator Theorems Exterior Angles Angles
Exterior Angles Sum Of A Triangle Exterior Angles Math Math Boards
Interior And Exterior Angles Of Polygons Ws Interior And Exterior Angles Exterior Angles Middle School Math Geometry
Math By Tori Triangles Unit Interior Angle Sum And Exterior Angle Remote Interior Angles Exterior Angles Theorems Math
Exterior Angle Sum Exterior Angles Mathematics Angles
Corollary To Triangle Angle Sum Theorem Exterior Angle Of A Triangle Exterior Angles Interior And Exterior Angles Exterior
This Image Gives You An Easy Way To Remember What A Quadrilateral Is Quadrilaterals Spacial Parallelogram
Angles And Polygons Interior And Exterior Angles Exterior Angles Interior Design School
