Exterior Angle Inequality Theorem Definition

What is the exterior angle property. The exterior angle theorem tells us that the measure of angle D is equal to the sum of angles A and B. Triangle Inequality Theorem The triangle inequality theorem states that any side of a triangle is always shorter than the sum of the other two sides.

cream exterior paint schemes construccion de escaleras exteriores contemporary design exterior construccion de jacuzzi exterior cream colored exterior shutters corvette c6 exterior door switch cost to paint a 1200 sq ft house exterior compra no cartao de cradito no exterior

Exterior Angle Inequality Theorem With Two Column Proofs Geometry Youtube

Exterior Angle Inequality Theorem Youtube

Exterior Angle Theorem Explanation Proof Examples

Exterior Angle Theorem Video Lessons Examples Step By Step Solutions

Theorems Of Inequality Video Lesson Transcript Study Com

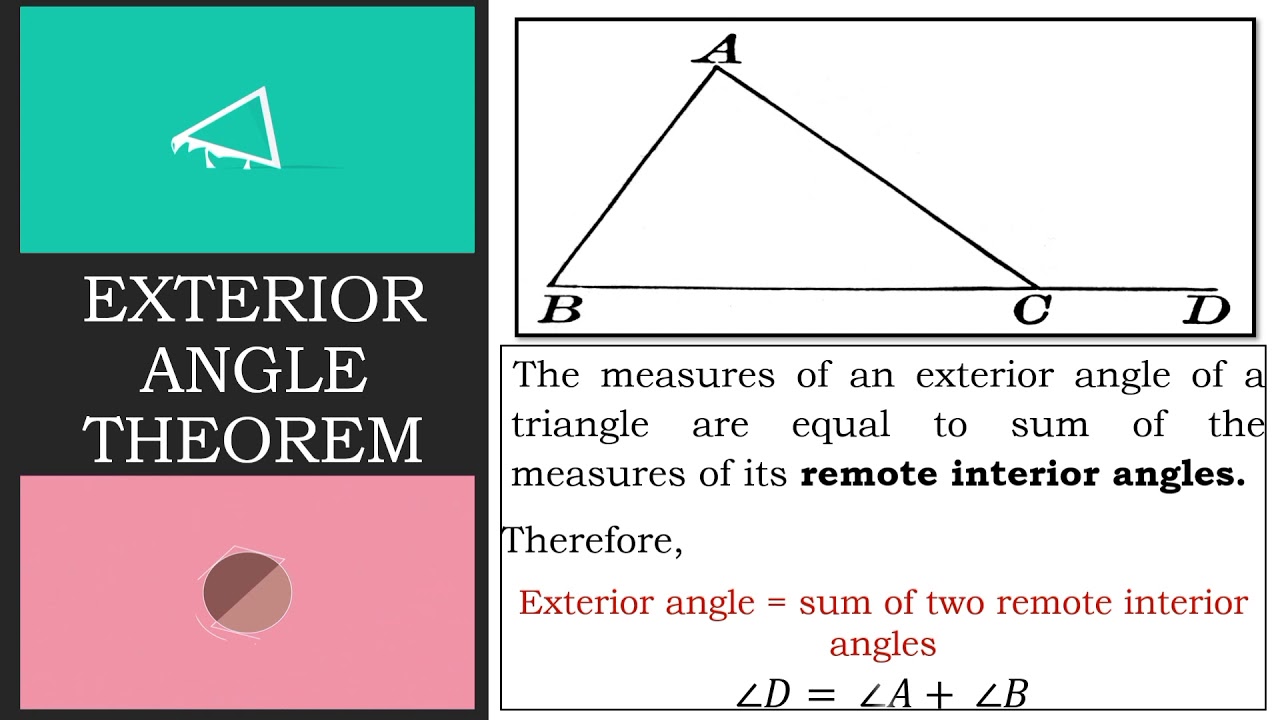
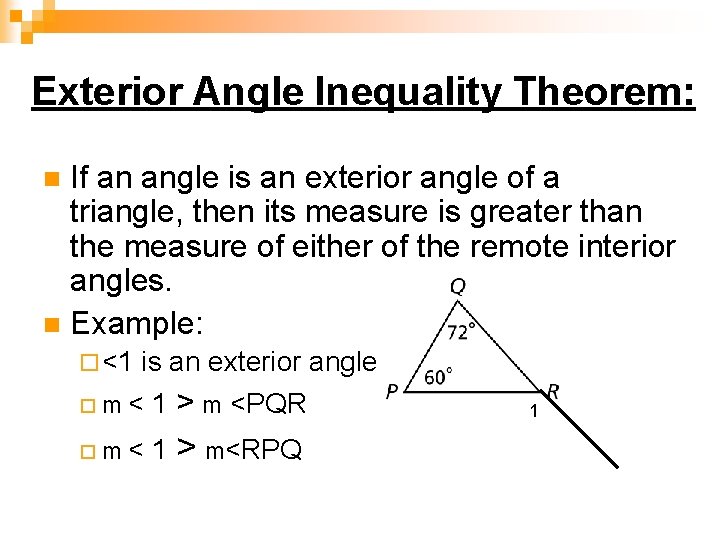
Geometry Chapter 5 2 And 5 4 Inequalities

By substitution the exterior angle is greater than the remote interior angle.

Exterior angle inequality theorem definition. An exterior angle of a triangle is greater than either of the non-adjacent interior angles. By the Exterior Angle Inequality Theorem the exterior angle is larger than either remote interior angle and Also and. According to the exterior angle inequality theorem the measure of an exterior angle of a triangle is greater than either of its interior opposite angles.

If a side of a triangle is produced then the exterior angle so formed is equal to. Therefore m 7 m 5 and m 8 m measures less than m 9 628721 By the Exterior Angle Inequality Theorem the exterior angle 9 is larger than either remote interior angle from two different triangles 6 and 7 from one. A similar argument proves it is greater than the other remote angle also.

As a result forms a linear pair with. By the Exterior Angle Inequality Theorem the exterior angle 5 is larger than either remote interior angle 7 and 8. Properties of exterior angles.

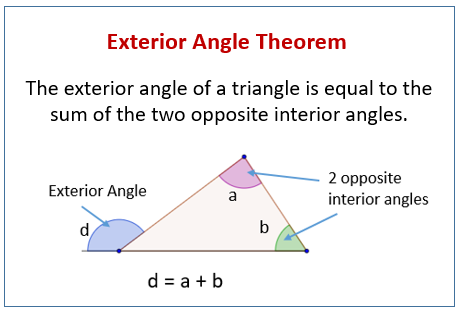
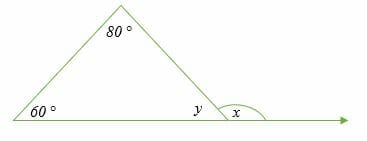
Theorem The Exterior Angle Inequality. The exterior angle theorem states that the exterior angle of a triangle is equal to the sum of the opposite interior angles. We can derive the exterior angle theorem using the information that.

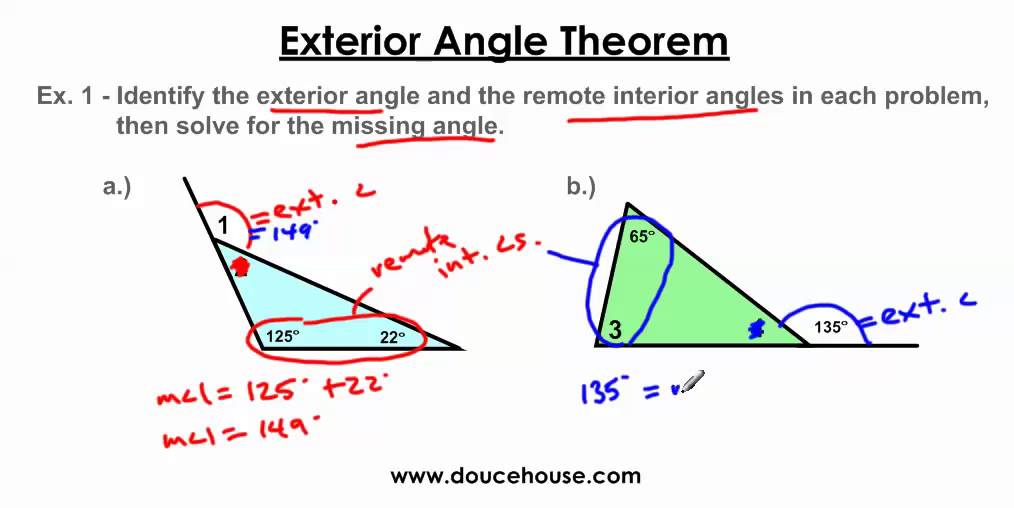
For example 5. An exterior angle of a triangle is formed when an side is extended outwards. By definition of inequality the exterior angle is greater than either part of its sum.

By extending of to a point is formed. We know that in a triangle the sum of exterior angles is equal to 360. The sum of an exterior angle and its adjacent interior angle is equal to 180 degrees.